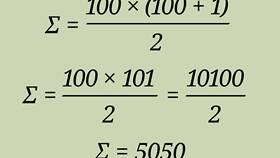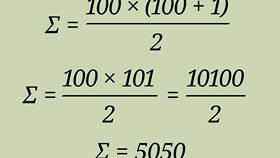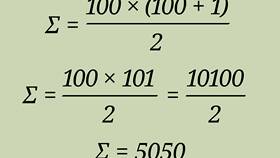Сумма всех натуральных чисел от 1 до 100 - классическая математическая задача, имеющая элегантное решение. Этот пример демонстрирует красоту математических закономерностей и часто используется для иллюстрации прогрессий.
Содержание
Сумма всех натуральных чисел от 1 до 100 - классическая математическая задача, имеющая элегантное решение. Этот пример демонстрирует красоту математических закономерностей и часто используется для иллюстрации прогрессий.
Решение задачи
Сумма чисел от 1 до 100 может быть вычислена по формуле суммы арифметической прогрессии:
| Формула | S = n(a₁ + aₙ)/2 |
| Где |
|
| Расчет | S = 100(1 + 100)/2 = 5050 |
Исторический метод Гаусса
Карл Фридрих Гаусс в детстве открыл оригинальный способ вычисления этой суммы:
- Записать числа от 1 до 100 и под ними от 100 до 1
- Сложить пары чисел (1+100, 2+99, 3+98 и т.д.)
- Каждая такая пара дает сумму 101
- Всего 100 пар, но мы удвоили исходную сумму
- Итог: (100 × 101)/2 = 5050
Математические свойства
- 5050 - треугольное число (100-е по счету)
- Является суммой первых 100 натуральных чисел
- Можно представить как 100×101/2
- Четное составное число
Обобщение формулы
Для суммы первых n натуральных чисел:
| Формула | Sₙ = n(n + 1)/2 |
| Примеры |
|
Практическое применение
Эта формула находит применение в различных областях:
- Анализ алгоритмов (вычисление сложности)
- Теория вероятностей
- Финансовые расчеты
- Физические вычисления
Таким образом, сумма всех натуральных чисел от 1 до 100 равна 5050. Это простое, но фундаментальное математическое соотношение, демонстрирующее эффективность математических методов для решения задач.
